周培源湍流理论概述

林建忠

(宁波大学机械工程与力学学院，宁波 315210)

(浙江大学航天航空学院，杭州 310027)

周培源先生1902年出生于江苏宜兴，1924年秋从清华学校高等科毕业后因成绩优秀被派送美国芝加哥大学继续完成大学课程，于1926年春、夏分别获学士和硕士学位。1927年春，周先生到美国加利福尼亚理工学院攻读博士学位，从事相对论研究，于1928年3月获理论物理博士学位。随后的几个月，周先生访问了哈佛大学、普林斯顿大学和康奈尔大学，并于1928年秋前往德国莱比锡大学跟随诺贝尔奖获得者海森堡教授（Heisenberg WK）从事量子力学研究，后来又应诺贝尔奖获得者泡利教授（Pauli WE）邀请，前往瑞士苏黎世联邦理工学院继续从事量子力学研究。1929年秋，周先生应国立清华大学罗家伦校长邀请，回国入职清华大学成为物理系教授，继续从事相对论研究。1936—1937年，周先生赴美国普林斯顿高等研究院从事相对论和宇宙论的研究，其间参加了爱因斯坦（Einstein A）组织的相对论研讨班。1937年，周先生从美国回国不久，“七七事变”引发了抗日战争的全面爆发，他认为作为一名科学家，应当以国家的利益为重，走科学救国之路，于是他毅然将主要精力从相对论的纯理论研究转向在抗战方面有应用价值的流体力学领域，从此开始长达半个多世纪的湍流研究。

以往通常将周培源湍流理论按时间分为四个阶段，即20世纪40年代、50～60年代、70年代、80～90年代。本文则将周培源湍流理论分为四个方面，即湍流“前模式理论”，涡旋结构的湍流统计理论，相似性理论和逐级逼近方法。

本文涉及的是不可压缩湍流场，构成湍流场的基本流体单元的运动遵循基本的物理规律，满足特定的数学方程。

1.1 基本方程

1.1.1 Reynolds平均运动方程

不可压缩湍流场基本流体单元满足的连续性方程和忽略体积力的Navier-Stokes方程为

式中ui和uj，p，ρ和ν分别是流体的速度、压力、密度和运动黏性系数；
xi是坐标。

Reynolds[1]认为，对充分发展的湍流场，可以将方程（1）（2）中速度和压力的瞬时量表示为平均量（大写字母）与脉动量（右上角带撇）之和

将其代入方程（1）（2）进行平均后可得

方程（5）称为Reynolds平均运动方程，式中的τij称为Reynolds应力，表示为

式中的“-”表示平均。对三维流场而言，Reynolds应力有9个分量（6个独立分量），这使得Reynolds平均运动方程（5）不封闭而无法求解。

早期的许多学者寻求各种途径解决方程的不封闭问题，途径之一是建立Reynolds应力与平均速度梯度的关系，如Prandtl[2]的混合长度理论，该理论定义流体单元迁移时保持原有动量的最大长度为混合长度，并将该长度类比于与流体黏性系数相关的分子自由程，从而建立Reynolds应力与平均速度梯度的关系；
Taylor[3]的涡旋传递理论，该理论与混合长度理论类似，区别在于用流体单元迁移时保持原有涡量的最大长度代替混合长度；
von Kármán[4]的局部相似性理论，该理论可以确定混合长度与空间坐标的关系。

以上封闭Reynolds平均运动方程的途径虽能用于对一些湍流场的描述，但有局限性，例如在平均速度梯度为零的湍流场中，Reynolds应力为零，这与实际不符。于是，解决方程不封闭问题的另一途径，就是建立导致方程（5）不封闭的Reynolds应力所满足的方程。

1.1.2 Reynolds应力方程

Reynolds将方程（3）代入方程（1）（2）后再减去方程（4）（5），得到脉动速度方程

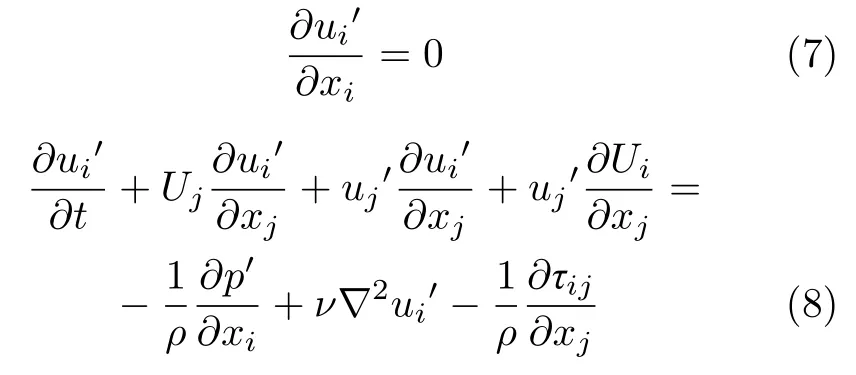
由方程（8）可以得到Reynolds应力（式（6））满足的Reynolds应力方程

该方程中包含的三阶脉动速度关联项、脉动压力梯度与脉动速度关联项、耗散项都是未知项，只有确定了这三项后才能使方程封闭求解。需要指出的是，在后来湍流模式理论的Reynolds应力模式中，通常将方程（9）写成

然后对方程中的湍流（或压力与湍流）扩散项、耗散项和压力变形项进行模化。

1.2 Reynolds应力方程的模化

1940年，周先生认为[5]，既然Navier-Stokes方程（2）是湍流场基本流体单元瞬时运动所满足的方程，那么仅考虑湍流的平均运动部分是不够的，湍流的脉动部分同样重要，必须同时考虑湍流脉动方程、Reynolds应力（二阶脉动速度关联）方程以及高阶脉动速度关联方程。于是，周先生对Reynolds应力方程（9）中包含的三个未知项分别进行以下的模化研究。Launder[6]称该研究为后来的湍流模式理论奠定了基础，所以在此将其称为湍流“前模式理论”。

1.2.1 三阶脉动速度关联项的模化

对于Reynolds应力方程（9）中未知的三阶脉动速度关联项，周先生进一步推导给出了三阶脉动速度关联方程[5]

可见三阶脉动速度关联方程（11）中又出现了四阶脉动速度关联和其他新的未知项。实际上，第n阶脉动速度关联方程中会出现第n+1阶脉动速度关联项。周先生认为，只有基于对脉动速度关联的物理假设，才能使一定阶的脉动速度关联方程得以封闭并求解。为此，他将方程（11）中的四阶脉动速度关联项用三个二阶脉动速度关联乘积之和表示

式中c是常系数，当时周先生基于脉动速度是时间或坐标的正弦函数这一假设给出c= 1/2，Heisenberg和Chandrasekhar后来也分别提出过该假设。受限于测量仪器和技术，式（12）在50年后通过对湍射流、湍尾流场的实验[7]得到证实，并给出射流场c= 1/2，尾流场c= 1的结论。

1.2.2 脉动压力梯度与脉动速度关联项的模化

（1） 脉动压力梯度与一项脉动速度关联项的模化

对于Reynolds应力方程（9）中脉动压力梯度与脉动速度的关联项，周先生假设脉动压力p"与平均压力有相同量级，给出了表达式[5]

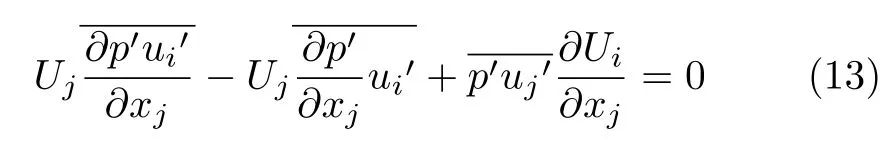
1945年，周先生对该项又做了进一步研究，他对脉动速度方程（8）取散度，根据连续性方程（4）和方程（7），得到脉动压力满足的Poisson方程[8]

进而得到脉动压力梯度满足的Poisson方程

该方程的解为

式中各量右上角的“*”号表示该量是积分域上任一点的量，不带“*”号的量表示脉动压力所在点的量（以下同）；
r是从脉动压力所在的点到积分域上任一点之间的距离；

dV∗和 dS∗分别是积分域的体积单元和面单元；
∂/∂n*表示法向导数。

周先生将方程（16）乘上脉动速度ul"后再平均，得到脉动压力梯度与脉动速度的关联

对不是很靠近壁面的区域而言，方程（17）最后一项面积分的被积函数很小，因而面积分可以忽略，在经过坐标变化和对被积函数中快变量与慢变量的分析之后，他给出方程（9）中的脉动压力梯度与脉动速度关联项[8]

（2） 脉动压力梯度与两项脉动速度的关联

对于三阶脉动速度关联方程（11）中脉动压力梯度与两项脉动速度的关联项，1940年，周先生假设该项可以近似地分解为依赖于平均压力梯度和不依赖于平均压力梯度的两个部分[5]

式中cijl和k(ijl)是常数但并不普适，可由实验确定，其中林家翘、胡宁等参加了确定k(ijl)的研究工作。

1945年，周先生对该项又做了进一步研究，采用与推导方程（17）相同的方法，得到脉动压力梯度与两项脉动速度的关联[8]

式（22）已经忽略了面积分的部分。对应于方程（18）～（20），周先生进一步给出了方程（11）中的脉动压力梯度与两项脉动速度关联项[8]

其中

1987年，周先生和陈十一[9]基于准相似性假设，将两个点的脉动速度关联函数用同一点的脉动速度关联以及脉动速度均方根的方次表示，给出了脉动压力梯度与脉动速度、两项脉动速度、三项脉动速度关联的表达式。

需要指出的是，周先生对于脉动速度与脉动压力梯度关联项的模化，与后来的湍流模式理论不同，后者是将该项分解成压力扩散项和压力变形项后分别进行模化[10]。

1.2.3 耗散项的模化

（1）二阶耗散项的模化

Reynolds应力方程（9）中含有二阶耗散项。1940年，周先生在对高Reynolds数压力驱动槽道湍流场的研究中忽略了该项，但他同时也指出，该项在一般湍流场中不可忽略。1945年，他在分析湍流场中相邻两点脉动速度特性的基础上，基于流场局部均匀条件，给出了方程（9）中包含非各向同性影响的二阶耗散项的表达式[8]

式中λ是Tarloy湍流微尺度，q是脉动速度的均方根，gik是度量张量的协变分量，k表示湍流场偏离各向同性的程度。同时，他还提出了方程（11）中三阶耗散项为0的近似。

（2）三阶耗散项的模化

三阶脉动速度关联方程（11）中含有三阶耗散项。1987年，周先生和陈十一基于准相似性假设，在方程（27）的基础上，推导得到了三阶耗散项的表达式[9]

式中c1和c2是待定常数。在该文中，他们还给出了四阶耗散项的表达式。

1.3 湍流“前模式理论”的应用

1.3.1 高Reynolds数压力驱动二维槽道流

1940年，周先生基于Reynolds平均运动方程（5）、Reynolds应力方程（9）、三阶脉动速度关联方程（11），对高Reynolds数压力驱动二维槽道流进行了求解[5]。求解时，方程（5）中忽略了黏性耗散项；
方程（9）中忽略了含黏性系数的耗散项，且脉动压力梯度与脉动速度的关联项用方程（13）表示；
方程（11）中忽略了含黏性系数的耗散项，且四阶脉动速度关联项用方程（12）表示，脉动速度梯度与两项脉动速度关联项用方程（21）表示。求解得到的平均速度分布与当时的实验结果相符合。

1.3.2 尾流及半射流

Reynolds平均运动方程（5）和Reynolds应力方程（9）分别用于对尾流[11]及半射流[12]的求解，其中方程（9）中脉动压力梯度与脉动速度的关联项，基于对称的条件用某一点或该点附近的值代替，而方程（9）中的耗散项表示为

式中k"是常数。求解得到的平均速度分布与实验结果相符合。

1.3.3 槽道、圆管和边界层流场

Reynolds平均运动方程（5）、Reynolds应力方程（9）、三阶脉动速度关联方程（11）分别用于对槽道[13]、圆管[14]、半无限平板边界层湍流场[15]的求解，其中方程（9）中的脉动压力梯度与脉动速度关联项用方程（18）～方程（20）表示，耗散项用方程（27）表示；
方程（11）中忽略四阶脉动速度关联项和耗散项，脉动压力梯度与两项脉动速度关联项用方程（23）～方程（26）表示。求解得到的平均速度分布与实验结果相符合。

自19世纪末开始，人们采用Reynolds提出的对Navier-Stokes方程先平均后求解的方法研究具有脉动特性的湍流场。正如第一部分所述，采用这种方法面临两大困难，一是方程组不封闭，为使方程组封闭，人们不得不提出一些假设，而这些假设往往缺乏普适性；
二是联立求解方程组的过程很复杂。

面对这两大困难，周先生对湍流场的求解又进行了深入的思考，他认为湍流运动与涡旋运动有着密切的联系，湍流由许许多多的涡旋组成，可以将最小尺度的涡作为湍流元。于是周先生和蔡树棠先生于1956年提出了先求解方程然后进行平均的方法[16]，即把求解Navier-Stokes方程得到的某个特定涡旋解（涡元）作为湍流元，再通过特定的统计平均方法得到湍流运动各种物理量的统计平均规律。34年后的1990年，Narasimha[17]指出，这种先求解后平均的方法是另一种传统的湍流研究方法，并特别强调所求的解就是湍流元。

2.1 线性化涡量方程及求解

这种先求解后平均方法的关键是寻找具体湍流场的涡元以及选择统计平均方法。

2.1.1 涡球运动解

1956年，周先生和蔡先生在忽略涡量动力学方程中非线性项的前提下，研究球形涡元的运动，得到了用汇合超几何函数表示的相似性解[16]

式中η是涡量，Ψ是流函数，U是球形涡元球面的移动速度，a是球形涡元半径，R和θ是极坐标，ν是流体黏性系数，t是时间。

由相似性解给出的流场涡量演变说明，初始集中在一个小体积内的涡元涡量会逐渐向外扩散，任意时刻围绕涡元中心存在一个由流面构成的圆球面，且该球面沿涡旋的对称轴移动。因流体黏性的作用，球面内外的涡量分布在球面上连续，涡元在运动过程中形状不变，但体积持续增大，涡元运动速度逐渐变小并趋向于零。他们还分析了相似性解的适用性，认为在涡元运动的初期，相似性解只在部分流场区域有效，而在涡元运动的后期，相似性解在整个流场有效。

2.1.2 均匀各向同性湍流后期的涡性结构

既然以上得到的相似性解适用于涡元运动后期的整个流场，而此时的流场可视为均匀各向同性，于是周先生和蔡先生同样在忽略涡量动力学方程中非线性项的前提下，得到了作为各向同性湍流元的球形涡元和一种轴对称涡元[18]

式中ui是涡元的诱导速度，U是涡元移动速度，lj是涡元轴线的方向余弦，a是涡元半径，R是极坐标，ν是流体黏性系数，t是时间。需要指出的是，Kovasznay等[19]于17年后发表了类似的结果。

他们基于涡元涡量集中在涡元中心附近且每个涡元总角动量为常数的假设，得到了均匀各向同性湍流场衰变后期的二阶速度关联函数解

式中n是单位体积中的涡元个数，其他符号的定义与方程（32）相同，该解与Batchelor等[20]的实验结果相符合。

他们还证明了涡元运动的涡性结构与湍流场的湍性结构密切相关，流线相似但涡量分布不同的涡元运动会导致不同的速度关联；
反之，流线不同但涡量分布相同的涡元运动则导致相同的速度关联。他们还提出，基于已知的涡元速度分布，可以计算高阶的速度关联函数。

黄永念先生[21]根据文献[18]给出的轴对称涡元速度场（32）和求速度关联的方法，计算了均匀各向同性湍流衰变后期的三阶速度关联，计算时把速度场表示成各向同性的张量形式

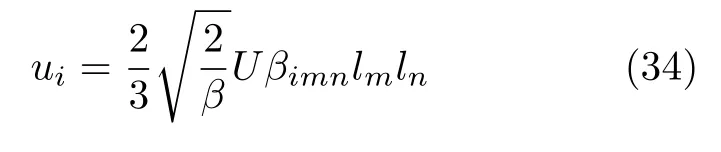
式中符号的定义与方程（32）（33）相同。

黄先生先采用多维Fourier变换推导三阶速度关联的谱函数，然后推导得到三阶速度关联

式中r是流场中两点距离，其他符号的定义与方程（32）（33）相同。由式（35）计算所得的结果与后来Bennett等[22]的实验结果相符合。

2.1.3 自由湍流的后期运动

在对均匀各向同性湍流后期涡性结构研究的基础之上，周先生和蔡先生把研究拓展到尾流、射流等具有剪应力的自由湍流场[23]。他们认为这类流场发展到远下游的特性与均匀各向同性湍流相似，可以采用研究均匀各向同性湍流的方法来研究自由剪切湍流场的后期运动，即基于湍流由涡元组成的想法求解自由剪切湍流场后期运动的方程。

首先，他们假设自由剪切湍流后期运动的湍流Reynolds数比较小，可以忽略脉动速度方程（8）中的非线性项，但须保留平均速度梯度项。其次，考虑到自由剪切湍流后期的涡旋尺度较小，可以认为涡旋尺度内的平均速度及其梯度保持不变。在以上两个前提下，他们求解脉动速度方程（8）得到了一种近似解，该解由湍流度比较高的均匀各向同性湍流的涡元运动和湍流度比较低的与平均速度梯度相关的涡元运动组成，而且前者大于后者。基于脉动速度的这一近似解，他们用文献[18]的平均方法，给出了湍流场中任一点的Reynolds应力张量[23]

式中n是单位体积中的涡元数；
A是积分常数，取决于具体流场；
t0为初始时刻；
ν是流体黏性系数；
U0为涡旋所在位置的速度。

他们将以上方法用于二维尾流远下游湍流场的求解，得到了平均速度分布、脉动速度平方的平均值以及Reynolds剪应力。

2.2 无黏涡量方程及求解

周先生认为[24]，既然可以用涡元运动对以上均匀各向同性湍流后期衰变的流场进行描述，那么也应当可以用涡元运动来描述均匀各向同性湍流初期和中期衰变时的流场以及具有剪应力的一般湍流场。

1965年，周先生等[25]研究高Reynolds数下的均匀各向同性湍流，根据高Reynolds数湍流场的特性，在文献[16]给出的涡量动力学方程中，忽略黏性项而保留非线性项，在球坐标下基于轴对称条件和采用分离变量法，得到了方程的自相似解。在此基础上，他们根据角动量守恒条件，得到了流场特征长度l、特征速度U与时间的关系[25]

式中l与涡旋尺度有关；
λ0和是初始时刻t=t0时的Tarloy湍流微尺度和湍流均方根速度，式（37）中l按t1/5的规律变化与实验结果[26]相符合。

他们还根据以上得到的自相似解，采用文献[18]的平均方法以及由Kármán-Howrth方程确定积分常数，得到二阶速度关联f和三阶速度关联k的表达式

式中B是无量纲常数，取决于具体流场；
其他符号的定义与方程（35）相同。

根据式（38）计算得到的结果，除坐标原点附近以外的大部分区域与实验结果[26-27]相符合。计算结果还表明，在二阶速度关联具有自相似性解的范围内，三阶速度关联的解不存在相似性。

在以上涡旋结构的湍流统计理论中，并非任意一个Navier-Stokes方程的解都可以作为湍流元，作为湍流元的解要满足涡旋角动量守恒条件和统计条件。周先生于1959年提出，这个统计条件就是流体力学中的相似性条件[28]，如同Prandtl在层流边界层理论中提出的相似性原理[29]。换言之，只有满足相似性解的涡元，才能作为涡旋结构湍流统计理论中的湍流元对湍流场进行统计平均，从而给出平均速度和各阶速度关联等统计量。

周先生认为，既然湍流平均运动速度存在相似性解，那么导致湍流脉动的无规涡元运动也应该存在相似性解；
如果存在相似性解，那么必定存在与相似性解相关的特征尺度；
Taylor称构成湍流最小涡旋（即涡元）的尺度为Taylor湍流微尺度λ，那么将λ作为与相似性解相关的特征尺度是自然的选择，况且在二阶耗散项方程（27）和三阶耗散项方程（28）中都包含λ。于是，建立湍流场的相似性理论，确定与相似性解相关的Taylor湍流微尺度λ，构成了周培源湍流理论的重要组成部分。

3.1 各向同性湍流中的湍流微尺度

既然Taylor湍流微尺度λ是最小涡旋的尺度，那么为了确定λ，可以从涡量方程入手。1945年，周先生对脉动速度方程（8）取旋度后得到脉动涡量方程[8]

1948年，周先生在方程（39）和方程（40）的基础上，建立了二阶脉动涡量关联满足的微分方程[30]。首先，他假设两个相邻点之间的二阶脉动速度关联和三阶脉动速度关联函数可以展开为两点位置矢量差与Taylor湍流微尺度λ之比的幂级数，且级数的系数是Reynolds应力的线性函数；
其次，假设关联函数相对于两点刚性平移的变化远小于两点相对位移引起的变化。根据以上两个假设，他将二阶脉动涡量关联方程中的各项进行模化，模化后产生6个标量方程，但未知量却有7个，即6个Reynolds应力分量和Taylor湍流微尺度λ。为此，他进一步假设，由对流携带的、通过垂直于流动方向单位面积的平均能量通量，正比于Reynolds应力在改变流体微元体积和形状时的功率在该方向上的梯度，反比于湍流能量衰减的平方。于是，他结合方程（27），将Reynolds应力方程（9）的指标缩并后得到湍流能量输运方程[30]

式中q2=uj′uj′，τmn如式（6）所示，D是与流场Reynolds有关的正常数，U0是流场特征速度，gij是度量张量的逆变分量，λ是Tarloy湍流微尺度。

基于以上方程，周先生研究各向同性湍流的能量和涡量衰减，给出了Tarloy湍流微尺度满足的关系[30]

式（42）与Batchelor等[31]的实验结果相符合。

他还基于脉动涡量方程（39），（40）和湍流能量输运方程（41），在忽略黏性耗散项的前提下求解了槽道湍流场，得到了近壁区域平均速度分布的对数律，且得到的脉动速度分量的均方值与实验结果定性一致。

3.2 脉动涡量的相似性解

周先生认为[28]，构成湍流脉动的涡元尺度Λ比较小，在Λ的范围内与涡元运动相关的函数（称快变量）在空间上有较大梯度，而平均速度和Reynolds应力（称慢变量）在空间上的梯度较小，因而可以把平均运动方程与脉动涡量方程（39）， （40）近似地分开求解。

他在求解脉动涡量方程（39），（40）时，采用以平均速度运动的动坐标系，该坐标系内的平均速度和Reynolds应力及其梯度只是动坐标系原点坐标的函数，然后引进关于脉动速度ui"的相似性条件[28]

式中Φi是相似性函数；
xi"是动坐标系的坐标；
Λ是涡元尺度，在相似性条件中起着重要作用；
q与Λ只是动坐标系原点坐标的函数，与xi"无关。

他将式（43）代入动坐标系下的脉动涡量方程，结合Reynolds平均运动方程（5），对二维槽道流、沿半无限平板流、圆管流、二维和轴对称尾流等湍流场进行了求解，得到了Reynolds应力与平均速度梯度之间的关系，从而给出与实验结果相符的平均速度、Reynolds应力等量的分布。

经过以上研究，周先生认为，以上的相似性解在一定范围内可以给出与实验结果符合的平均速度、Reynolds应力等量的分布，但涡元尺度Λ并非普适，在二维槽道流、沿半无限平板流和圆管流等有壁面约束的流场中，Λ与von Kármán相似理论中的混合长度相同，此时Λ只与平均速度梯度有关，与流体黏性无关；
而在二维和轴对称尾流等不受壁面直接影响的流场中，Λ与流体黏性有关，此时Λ与Tarloy湍流微尺度λ有相同性质。因此，Λ与λ的关系要通过求解相似性变换的非线性涡量脉动方程后再计算脉动速度关联予以确定。

以上虽然给出了湍流场的相似性解，但在不同的流场甚至在同一流场不同的区域，将存在不同的相似性解，需要进一步建立流场不同区域之间相似性解的关系。

3.3 准相似性理论

3.3.1 低Reynolds数均匀各向同性湍流场

在2.1.2中，周先生和蔡先生曾将均匀各向同性湍流视为由许多同一种轴对称涡元组成，这些涡元的位置和取向随机分布[18]。经过多年的观察和分析，1975年，周先生和黄永念先生[32]认为，涡元在衰变过程中会出现伸缩现象，其结构并不具有简单的相似性。为此，他们假设每个涡元足够小，涡量集中在涡元中心附近，每个涡元在运动中保持自身的速度而不受其他涡元的影响，同时引进涡旋Reynolds数Ra=Ua/ν （U和a分别是涡元的特征速度和特征长度）来表征涡元的衰变特征，它与流场Reynolds数Rλ=λ/ν（是湍流脉动速度均方根，λ是Tarloy湍流微尺度）不同，Ra的值取决于涡元结构，而Rλ的值则取决于湍流场的衰变特征。

然后，他们对Navier-Stokes方程取旋度得到涡量方程，将方程应用于轴对称涡元后得到相应的涡量方程组。涡元在衰变过程中的伸缩会导致涡元尺度和结构随时间改变时呈现不同的变化规律，因此要建立湍流场整个衰变过程中涡元特征长度（即相似性尺度）和结构随时间变化的关系。

为了使涡量方程组可解，他们先建立涡元尺度a和Ra的关系。考虑到在湍流衰变后期，Ra的值很小，涡量方程组中包含Ra的项可以忽略，此时涡量方程组存在相似性解的条件是(a/ν)·(da/dt)为常数；
而在湍流衰变初期，Ra的值较大，涡量方程组中的黏性项可以忽略，此时方程组存在相似性解的条件是(a/ν)(da/dt)正比于Ra。鉴于以上两种极端情况，他们给出了湍流衰变初期到后期a与Ra满足的关系式[32]

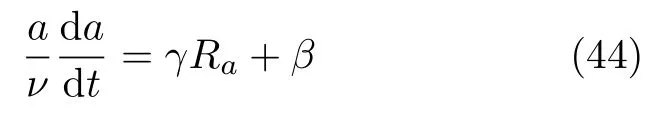
式中γ和β是待定常数，可以被组合进平均速度U和涡元特征长度a中而成为

他们将式（45）代入涡量方程组，由尺度变换体现涡元结构的伸缩，在低Reynolds数前提下，得到了用汇合超几何函数表示的线性零级近似方程的准相似性解，且计算得到了Tarloy湍流微尺度λ的表达式[32]

式中符号与式（44）相同。

在式（46）和式（44）的基础上，他们给出了湍流衰变后期的λ2= 4νt，该结果与1957年在均匀各向同性湍流衰变后期流场中的结果[18]相同；
给出了湍流衰变初期的λ2= 10νt，该结果与1948年在各向同性湍流中给出的表达式（42）[30]相对应，这些结论被后来的实验结果[33]所证实。

此外，他们还给出了从湍流衰变初期到后期的湍能衰变规律和二阶速度关联值，结果与实验结果[34]基本符合。

3.3.2 均匀各向同性湍流场

以上的准相似性解只适用于低Reynolds数均匀各向同性湍流场，所以得到的二阶速度关联值在湍流衰变初期比实验值[34]小。1981年，周先生和黄先生[35]进一步引进一个湍流能量条件

式中c为常数，U和a分别是涡元特征速度和特征长度。

他们基于Ra=Ua/ν，式（45）和式（47），涡元角动量守恒条件以及Tarloy湍能衰变方程，将涡旋的涡量和流函数展开成Legendre多项式微商的级数，以此求解Navier-Stokes方程，得到了一组以时间t和径向坐标为独立变量的无穷多个非线性偏微分方程，接着在零级近似下用Fourier变换将这组方程由物理空间变换到谱空间，然后求解从湍流衰变初期到后期的整个流场，得到的能谱函数E0和能谱交换函数W0精确地满足谱空间的Kármán-Howrth方程

式中k是三阶速度关联，ν是黏性系数。

他们还计算得到了Tarloy湍流微尺度λ与涡元特征尺度a的关系、涡旋Reynolds数Ra与流场Reynolds数Rλ的关系[35]

式中n是单位体积中的涡元个数，C0是角动量常数，ν是黏性系数。

由式（49）可见，在湍流衰变初期Ra很大时，a远大于λ；
在湍流衰变后期Ra很小时，a与λ的值相当，说明涡元在湍流衰变初期和后期分别代表大尺度涡和小尺度涡。当Ra很大时，由（49）的第二式可知Rλ近似为常数，这与湍流衰变初期的实验结果[34]相符合。

此外，他们给出的湍能衰变、积分尺度、二阶脉动速度关联都与实验结果[20,26,36-37]相符合。

3.4 广义准相似性理论

以上的相似性理论和准相似性理论只能应用于均匀各向同性湍流场。1985年，周先生将用于均匀各向同性湍流场的准相似性理论（45）推广到具有剪应力的一般湍流场[38]

式中λ是Tayloy湍流微尺度；
Ωik见式（40）；
R0，R1，k1，k2是常数。

式（50）称为广义准相似性条件，右边方括弧中保留第一、二项而去掉第三项，就是Prandtl的混合长度理论；
保留第二项而去掉第一、第三项，就是Taylor的涡旋传递理论；
保留第二、第三项而去掉第一项，就是von Kármán的局部相似性理论。

他给出的相似性解[38]为

在这样的相似性解下，方程（19）和方程（20）可以化为简单的形式，将简化的形式代入方程（18）就得到Reynolds应力方程（9）中脉动压力梯度与脉动速度关联项的表达式，然后将方程（9）的耗散项采用方程（27）表示，忽略方程（9）中的三阶脉动速度关联项，由此得到可以进行求解的一组封闭方程组。将该方程组用于压力驱动二维槽道湍流[38]、平面湍尾流[39]、平面湍射流[40]、轴对称湍射流[41]的求解，得到的平均速度、脉动速度二阶关联、Tarloy湍流微尺度λ与实验结果[42]相符合。

1987年，陈十一和周先生[43]在文献[38]的基础上，提出分别用耗散尺度和含能尺度来描述湍流场，其中耗散尺度为Tarloy湍流微尺度λ，可由方程（50）的广义准相似性条件描述；
含能尺度则利用两点关联在局部均匀的条件下推导得到。基于这两种尺度，他们对均匀单向剪切湍流场求解了二阶脉动速度关联方程，得到了相同Reynolds数不同剪切率下的二阶脉动速度关联以及这两种尺度的衰变规律，计算结果与实验结果[44-45]相符合。

第一部分中提到的湍流“前模式理论”给出了求解湍流场的一条途径，由于湍流场的复杂性以及限于当时的计算条件，如1.3中所述，该途径只能在一些假设下对简单的湍流场求一些近似解。

1945年，周先生曾提出过同时直接求解Reynolds平均运动方程（5）和脉动速度方程（8）的观点[8]，后来该观点又有了发展[38]，即建立逐阶的脉动速度关联方程，然后结合Reynolds平均运动方程进行求解，这就是求解湍流场的另一条途径-逐级逼近法。与第一条途径相比，该途径可以得到高阶的脉动速度关联，从而可以求解满足准相似性条件的一般剪切湍流场。1936～1937年，周先生在普林斯顿高等研究院研究期间，Einstein在其助手帮助下，根据引力方程与谐和条件，用逐级逼近法建立了多体运动理论，这给周先生建立湍流研究中的逐级逼近法很大启发。

4.1 奇阶截断法

4.1.1 原理

如前所示，各阶脉动速度关联方程都是很复杂的偏微分方程，在对方程中的某些项进行模化后，还可能成为积分-微分方程。在建立逐阶的脉动速度关联方程后，如果直接将所有阶的脉动速度关联方程联立求解，会使计算过程变得很复杂。

于是，周先生在对湍流场特性进行深入分析后，提出了奇阶截断法[9]，该方法的根据是：脉动速度关联的阶数越高，对流场的湍动特性影响越小；
奇数阶的脉动速度关联值比邻近阶的偶数阶脉动速度关联值小，例如三阶关联比二阶关联小、五阶关联比四阶关联小。所以，在求解偶数阶脉动速度关联方程时，可以把方程中的奇数阶脉动速度关联项略去。

根据奇阶截断的阶数不同，可以产生不同级的近似解，由Reynolds平均运动方程（5）和略去三阶脉动速度关联项的Reynolds应力方程（9）联立求出的解，称为一级近似解；
将一级近似解作为已知量，代入到三阶脉动速度关联项方程和略去五阶脉动速度关联项的四阶脉动速度关联方程中，联立求出的解称为二级近似解。

4.1.2 应用

一级近似解的方法在早期已被采用。作为一级近似解，文献[11-12]得到了与实验符合较好的尾流及半射流湍流场的平均速度。文献[38]得到了与实验符合较好的二维槽道湍流场和平面湍尾流场的平均速度、脉动速度二阶关联和Tarloy湍流微尺度λ。文献[46]对存在自相似性的平面混合层后期湍流场，得到了与实验结果[47-48]相符合的平均速度、二阶脉动速度关联以及Tarloy湍流微尺度λ。

作为二级近似解，文献[9]得到了平面湍尾流的脉动速度三阶关联和四阶关联，其中三阶脉动速度关联值与实验[49-50]和理论结果[10]相符合，四阶关联脉动速度值被后来的实验结果[7]所证实。

4.2 逐级迭代法

4.2.1 原理

奇阶截断法对高阶脉动速度关联方程的截断是合理的，而且应用于一些湍流场也是可行的。但周先生认为，尽管该方法略去了奇数阶脉动速度关联方程，但留下的偶数阶脉动速度关联方程仍然很复杂，原因是这些方程仍是非线性的积分微分方程，而且方程中包含与平均量相关的慢变量和与脉动量相关的快变量，对时域的分辨率要求很高，导致逐阶地求解高阶脉动速度关联方程比较费时。

于是，他进一步提出了逐级迭代法（又称逐级逼近法），该方法的思路是：由准相似性条件出发，对Reynolds平均运动方程（5）和略去三阶脉动速度关联项的Reynolds应力方程（9）联立求解，得到平均速度和Reynolds应力，将其代入湍流脉动速度方程（8）中求解脉动速度，对求得的脉动速度计算二阶关联得到二级近似的Reynolds应力，再将该应力代入Reynolds平均运动方程（5）中求解二级近似的平均速度···。用该方法不仅可以求出需要的湍流平均量和二阶关联函数，还可以便捷地计算高阶脉动速度关联函数。此外，采用逐级迭代法可以避免求解高阶脉动速度关联方程带来的困难，且求解脉动速度方程可以采用常规的快速Fourier变换等方法，比较容易实施。

4.2.2 应用

Lin等[51]对于平面湍尾流场，将奇阶截断法中得到的平均速度和Reynolds应力作为一级近似解[38]代入湍流脉动速度方程，采用谱方法数值求解该方程，然后对求解得到的脉动速度求各阶关联，得到了与实验结果[50]相符合的二阶、三阶和四阶脉动速度关联函数。

Wang等[52]对不同Reynolds数的均匀各向同性湍流场，将脉动速度等物理量用Fourier级数展开，把物理空间上的量转化到谱空间上计算，给出的二阶和三阶脉动速度关联、湍流能谱函数、湍流Reynolds数以及广义Tarloy湍流微尺度与实验结果[20,26]相符合。

Lin等[53]对于槽道湍流场，联立求解Reynolds平均运动方程和忽略三阶关联的二阶脉动速度关联方程，将求得的平均速度和Reynolds应力代入湍流脉动速度方程，然后用谱方法和有限差分法数值求解该方程，对求得的脉动速度计算各阶关联后得到的Reynolds应力、三阶和四阶脉动速度关联函数与实验结果[54-55]相符合。

孟庆国等[56]对于平面湍流混合层，将奇阶截断法中得到的平均速度和Reynolds应力作为一级近似解[8,38]代入湍流脉动速度方程，对求解该方程得到的脉动速度求平均，给出二阶近似的Reynolds应力，将其代入Reynolds平均运动方程求解二阶近似的平均速度，最后再将二阶近似的平均速度和Reynolds应力代入湍流脉动速度方程中求出脉动速度，对脉动速度求平均给出的二阶、三阶、四阶脉动速度关联函数与实验结果[7,47]相符合。

范萌等[57]对于平面湍射流场，基于一级近似解的平均速度和Reynolds应力，求解湍流脉动速度方程，对得到的脉动速度求平均给出的二阶、三阶、四阶脉动速度关联函数与实验结果[7]相符合。

（1）1951年，Rotta提出了湍流二阶矩封闭模型，该模型通常被认为是湍流模式理论的起源。而早在1940年，周先生就提出求解湍流场必须同时考虑脉动方程、Reynolds应力方程和高阶脉动速度关联方程，并开始了对Reynolds应力方程中所包含未知项的模化研究。所以，国际著名流体力学家Launder和Lumely称周先生为湍流模式理论的奠基人乃名副其实。

（2）1956年，周先生提出了涡旋结构湍流统计理论，该理论与目前流行的湍流直接数值模拟有共同之处，即都是先求方程的解然后由统计平均给出二阶和高阶脉动关联量，不同的是前者求方程的解析解或近似解析解，后者借助计算机求方程的数值解，可谓殊途同归。

（3）1985年，周先生将用于均匀各向同性湍流的准相似性理论推广到具有剪应力的一般湍流场，建立了广义准相似性理论，该理论具备了Prandtl混合长度理论、Taylor涡旋传递理论和von Kármán局部相似性理论的描述功能，对湍流场尺度结构给出了更综合的刻画，可谓匠心独具。

（4）周先生于20世纪80年代提出的逐级逼近法将湍流场的快变量与慢变量分开求解，通过求解快变的脉动速度方程，逐步逼近慢变的平均量和统计量的真实解。该方法不仅能便捷地给出湍流场高阶脉动速度关联函数的信息，从而更深入地了解流场特性，而且对当今数值模拟湍流场中减少计算量有参考价值，逐级逼近法与大涡模拟方法都是将不同尺度的涡分别处理，可谓异曲同工。

（5）周先生从20世纪30年代末开始从事湍流研究一直到90年代初，历经半个多世纪。他40年代建立了湍流“前模式”理论，50年代建立了涡旋结构湍流统计理论和湍流场后期衰变的相似性理论，60年代提出了湍流场前期衰变的相似性理论，70年代提出了准相似性理论，80年代提出了广义准相似性理论和逐级逼近法。每个年代都有创新性成果，为湍流研究做出了突出的贡献 。Lumley教 授 将 周 先 生 与 von Kármán、Kolmogorov、Taylor并称为四位流体力学的巨人乃实至名归。

猜你喜欢涡量周先生三阶三阶非线性微分方程周期解的非退化和存在唯一性数学物理学报(2022年2期)2022-04-26含沙空化对轴流泵内涡量分布的影响中国农村水利水电(2021年2期)2021-03-05戴着耳塞生活的人心理与健康(2018年7期)2018-05-14自由表面涡流动现象的数值模拟能源研究与信息(2018年1期)2018-05-08新型三阶TVD限制器性能分析北京航空航天大学学报(2017年4期)2017-11-23岁月如歌，师恩难忘—纪念周小燕先生一百周年诞辰歌唱艺术(2017年10期)2017-05-18巧填三阶幻方中学生数理化·七年级数学人教版(2017年2期)2017-03-25细腻不等于多情中国新闻周刊(2016年26期)2016-10-27航态对大型船舶甲板气流场的影响中国舰船研究(2015年3期)2015-02-07礼必须到党建文汇·上(2014年11期)2015-01-28